di Umberto Morini
In ogni momento della risoluzione di un sudoku, i candidati sono numeri che possono essere inseriti in una casella. Rimandiamo invece la definizione delle coppie, perché è meglio spiegarle prima con esempi. Nella risoluzione guidata di questo sudoku ne vedremo l’uso.
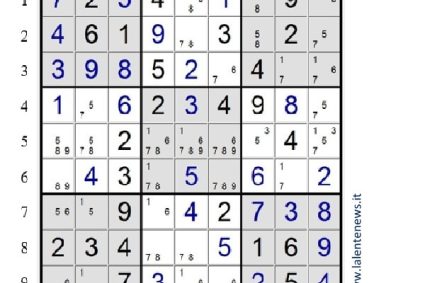
Di solito si comincia con gli slittamenti, ma la particolarità di questo sudoku è la presenza di sei numeri nei settori I e IX: è un invito a completarli. Solo il IX si completa subito con 9h=5, 8h=6, 8g=1. Passiamo agli slittamenti: 3 in II e 2f=3, 4 in VII e 8c=4, 5 in II e 3d=5. Per l’eliminazione di otto numeri su nove si ha 3g=4. Seguono altri slittamenti: 4 in II, 4 in VI (o in colonna h) e 5h=4, 4 in V, 9 nella riga 4 (4g=9), 9 in III (1h=9), 2 nella riga 1 (1b=2) che permette di completare il settore I con 2b=6 e 2c=1; slittamento di 2 nella riga 4 (4d=2), di 2 in III, VIII, VII, IV, di 3 in VII e IV. In 7c con l’eliminazione di otto numeri su nove si ha 7c=9 e quindi 9c=7.
Dopo aver terminato l’uso delle tecniche elementari, che individuano il numero esatto in una casella, entrano in gioco i candidati. Dobbiamo scrivere a matita, in piccolo, all’interno di ogni casella vuota tutti i suoi candidati e bisogna usare molta attenzione: dimenticarne uno o scriverne uno in più, estraneo, può causare errori nella risoluzione.
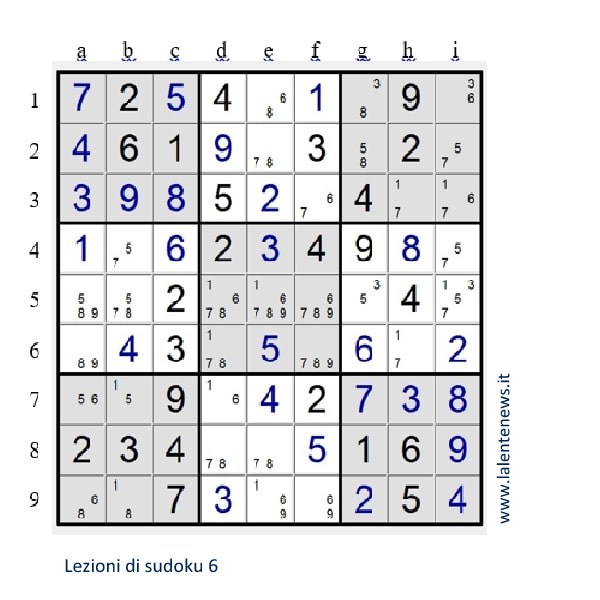
Non esiste un solo modo di procedere. Cominciamo per esempio dai settori che hanno meno caselle vuote. Nel settore II mancano i numeri 6, 7, 8: escludendo per ogni casella i numeri che possono slittare su di essa, i candidati sono 6 e 8 per 1e, 7 e 8 per 2e, 6 e 7 per 3f.
Si può anche considerare ogni numero mancante in un settore e scriverlo come candidato nelle caselle in cui non può slittare: nel settore IV il 5 slitta in 6a e si scrive nelle altre tre caselle, il 7 slitta in 5a e 6a ed è candidato in 4b e 5b, 8 si scrive in 5a, 5b e 6a, 9 in 5a e 6a.
Consideriamo ora il settore VIII. Le due caselle 8d ed 8e hanno entrambe i due candidati 7 ed 8 (come si vede nella riga 8) e si forma una coppia nel settore, che esclude 7 ed 8 dai candidati delle altre tre caselle: infatti se si collocasse 8 in 9e od in 9f, la riga 8 non si potrebbe più completare.
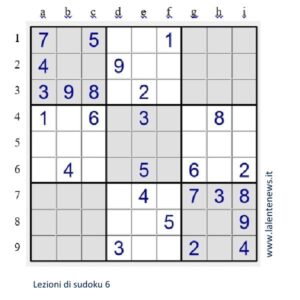
Proseguendo la scrittura dei candidati si arriva alla situazione della figura seguente.
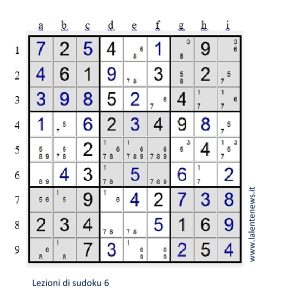Consideriamo ora la colonna e. Le due caselle 2e e 8e hanno solo i candidati 7 ed 8 e formano una coppia in e: nessun’altra casella della colonna può contenere i candidati 7 od 8, che debbono essere cancellati in 1e e 5e; dunque si ha 1e=6. Dopo aver scritto il 6, bisogna eliminarlo dai candidati delle caselle nelle quali può slittare, che sono 3f, 1i, 5e, 9e. Poi 3f=7 (o 1i=3) e si cancella il 7 (o il 3) nelle caselle in cui non è più candidato; la risoluzione si termina facilmente.
